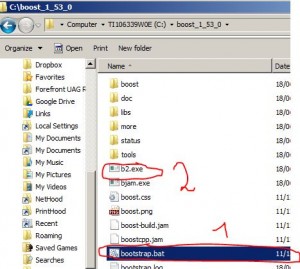
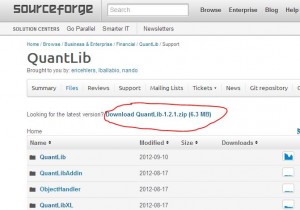
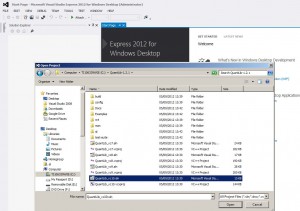
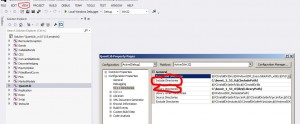
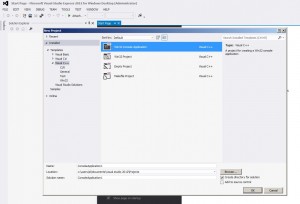
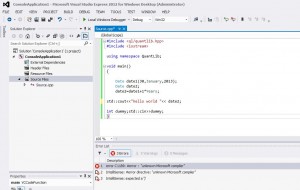
Aquí mostraremos un ejemplo de calculo de CVA (credit valuation adjustment, ajuste por riesgo de credito ) para un portafolio de derivados financieros que consiste en un solo swap con Formula de de Basilea iii .También es requerido calcularlo por IFRS 13.Usaremos el método Monte-Carlo y Programa en python con modulo de librería QuantLib .
Algoritmo de calculo de CVA (ajuste riesgo de crédito)
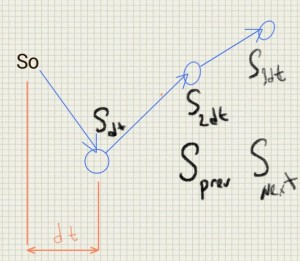
1) simular la curva de tipos para las fechas futuras.
2) calcular NPV (fair value) de portafolio de swaps para cada escenario en cada fecha futura.
3) calcular CVA como suma de EE (expected Exposure) multiplicada por probabilidad de default en cada intervalo según la formula:
$$ CVA = (1-R) \int{DF(t) EE(t) dQ_t} $$
R – Recovery
DF(t) – Factor Descuento
1) en este ejemplo usaremos modelo Hull White de 1 factor para simular la evolucion de la curva en futuro.
modelo de Hull-White tiene la siguiente dinámica para tipo de interés instantáneo $$ r_t $$
$$ dr_t=(\theta_t-ar_t)dt+\sigma dW_t $$
$$ r_t $$ esta distribuido como gaussiana con esperanza y variance condicionados:
$$ E(r_t|r_s)=r_se^{-a(t-s)}+\gamma_t-\gamma_se^{-a(t-s)}$$
$$ Var(r_t|r_s)=\frac{\sigma^2}{2a}(1-e^{-2a(t-s)})$$
donde:
$$ \gamma_t=f_t(0)+\frac{\sigma^2}{2a}(1-e^{-at})^2 $$
2) Para cada fecha futura calcularemos la forma de curva de tipos.
para construir la curva para cada valor de $$ r_t $$ usaremos factores descuento de Hull-White
$$ P_{->T}(t)=A(t,T)e^{-B(t,T)r_t} $$
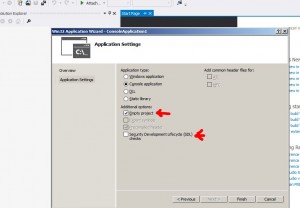
3) para aproximar CVA usaremos la formula de Basilea III
$$ CVA= (1-R) \sum \frac{EE^{*}_{T_{i}}+EE^{*}_{T_{i-1}}}{2} (e^{-\frac{ST_{i-1}}{1-R}}-e^{-\frac{ST_{i}}{1-R}})^+ $$
En este ejemplo suponemos 500bps constant Credit Default Swap CDS spread.
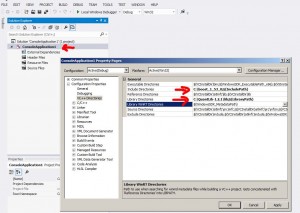
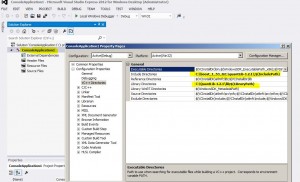
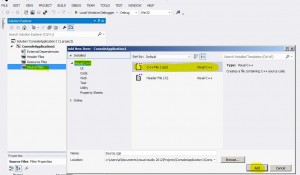
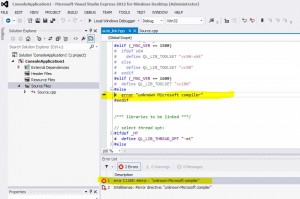
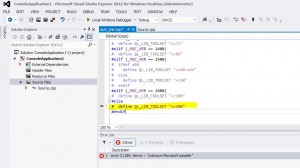
Código Python para calculo de CVA
Como swap de tipos de interés cojemos
nominal SWAP 10MM EUR
Receiver 5% cada 6 meses
pata fija y pata flotante con day counter Actual/360.
Calendario TARGET.
#(c) 2013 PriceDerivatives.com
# Distributed without any warranty
from QuantLib import *
import numpy as np
from math import *
from pylab import *
def A(t,T):
forward = crvToday.forwardRate(t, t,Continuous, NoFrequency).rate()
value = B(t,T)*forward - 0.25*sigma*B(t,T)*sigma*B(t,T)*B(0.0,2.0*t);
return exp(value)*crvToday.discount(T)/crvToday.discount(t);
def B(t,T):
return (1.0-exp(-a*(T-t)))/a;
def gamma(t):
forwardRate =crvToday.forwardRate(t, t, Continuous, NoFrequency).rate()
temp = sigma*(1.0 - exp(-a*t))/a
return (forwardRate + 0.5*temp*temp)
def gamma_v(t):
res=np.zeros(len(t))
for i in xrange(len(t)):
res[i]=gamma(t[i])
return res
Nsim=100
a=0.1
sigma=0.02
todaysDate=Date(30,12,2013);
Settings.instance().evaluationDate=todaysDate;
crvToday=FlatForward(todaysDate,0.02,Actual360())
r0=forwardRate =crvToday.forwardRate(0,0, Continuous, NoFrequency).rate()
months=range(1,12*5,1)
sPeriods=[str(month)+"m" for month in months]
Dates=[todaysDate]+[todaysDate+Period(s) for s in sPeriods]
T=[0]+[Actual360().yearFraction(todaysDate,Dates[i]) for i in xrange(1,len(Dates))]
T=np.array(T)
rmean=r0*np.exp(-a*T)+ gamma_v(T) -gamma(0)*np.exp(-a*T)
np.random.seed(1)
stdnorm = np.random.standard_normal(size=(Nsim,len(T)-1))
rmat=np.zeros(shape=(Nsim,len(T)))
rmat[:,0]=r0
for iSim in xrange(Nsim):
for iT in xrange(1,len(T)):
mean=rmat[iSim,iT-1]*exp(-a*(T[iT]-T[iT-1]))+gamma(T[iT])-gamma(T[iT-1])*exp(-a*(T[iT]-T[iT-1]))
var=0.5*sigma*sigma/a*(1-exp(-2*a*(T[iT]-T[iT-1])))
rmat[iSim,iT]=mean+stdnorm[iSim,iT-1]*sqrt(var)
startDate=Date(30,12,2013);
crvMat= [ [ 0 for i in xrange(len(T)) ] for iSim in range(Nsim) ]
npvMat= [ [ 0 for i in xrange(len(T)) ] for iSim in range(Nsim) ]
for row in crvMat:
row[0]=crvToday
for iT in xrange(1,len(T)):
for iSim in xrange(Nsim):
crvDate=Dates[iT];
crvDates=[crvDate]+[crvDate+Period(k,Years) for k in xrange(1,21)]
crvDiscounts=[1.0]+[A(T[iT],T[iT]+k)*exp(-B(T[iT],T[iT]+k)*rmat[iSim,iT]) for k in xrange(1,21)]
crvMat[iSim][iT]=DiscountCurve(crvDates,crvDiscounts,Actual360(),TARGET())
#indexes definitions
forecastTermStructure = RelinkableYieldTermStructureHandle()
index = Euribor(Period("6m"),forecastTermStructure)
#swap 1 definition
maturity = Date(30,12,2018);
fixedSchedule = Schedule(startDate, maturity,Period("6m"), TARGET(),ModifiedFollowing,ModifiedFollowing,DateGeneration.Forward, False)
floatingSchedule = Schedule(startDate, maturity,Period("6m"),TARGET() ,ModifiedFollowing,ModifiedFollowing,DateGeneration.Forward, False)
swap1 = VanillaSwap(VanillaSwap.Receiver, 1000000,fixedSchedule,0.05 , Actual360(),floatingSchedule, index, 0,Actual360()) #0.01215
for iT in xrange(len(T)):
Settings.instance().evaluationDate=Dates[iT]
allDates= list(floatingSchedule)
fixingdates=[index.fixingDate(floatingSchedule[iDate]) for iDate in xrange(len(allDates)) if index.fixingDate(floatingSchedule[iDate])<=Dates[iT]]
if fixingdates:
for date in fixingdates[:-1]:
try:index.addFixing(date,0.0)
except:pass
try:index.addFixing(fixingdates[-1],rmean[iT])
except:pass
discountTermStructure = RelinkableYieldTermStructureHandle()
swapEngine = DiscountingSwapEngine(discountTermStructure)
swap1.setPricingEngine(swapEngine)
for iSim in xrange(Nsim):
crv=crvMat[iSim][iT]
discountTermStructure.linkTo(crv)
forecastTermStructure.linkTo(crv)
npvMat[iSim][iT]=swap1.NPV()
npvMat=np.array(npvMat)
npvMat[npvMat<0]=0
EE=np.mean(npvMat,axis=0)
S=0.05 #constant CDS spread
R=0.4 #Recovery rate 40%
sum=0
#calculate CVA
for i in xrange(len(T)-1):
sum=sum+0.5*(EE[i]*crvToday.discount(T[i])+EE[i+1]*crvToday.discount(T[i+1]))*(exp(-S*T[i]/(1.0-R))-exp(-S*T[i+1]/(1.0-R)))
CVA=(1.0-R)*sum
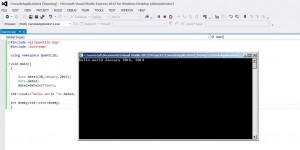
print "\nCVA=",CVA
plot(T,EE)
print "\nEE\n",npvMat
show()
Output
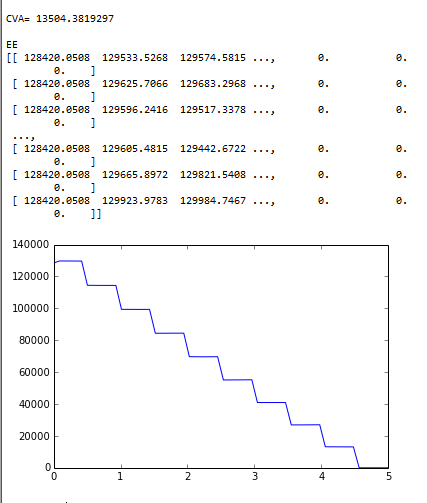
CVA expected exposure swap
![[<<] PriceDerivatives](http://www.pricederivatives.com/es/wp-content/uploads/2014/03/cropped-pricederivatives-blog-logo-Copy11.png)