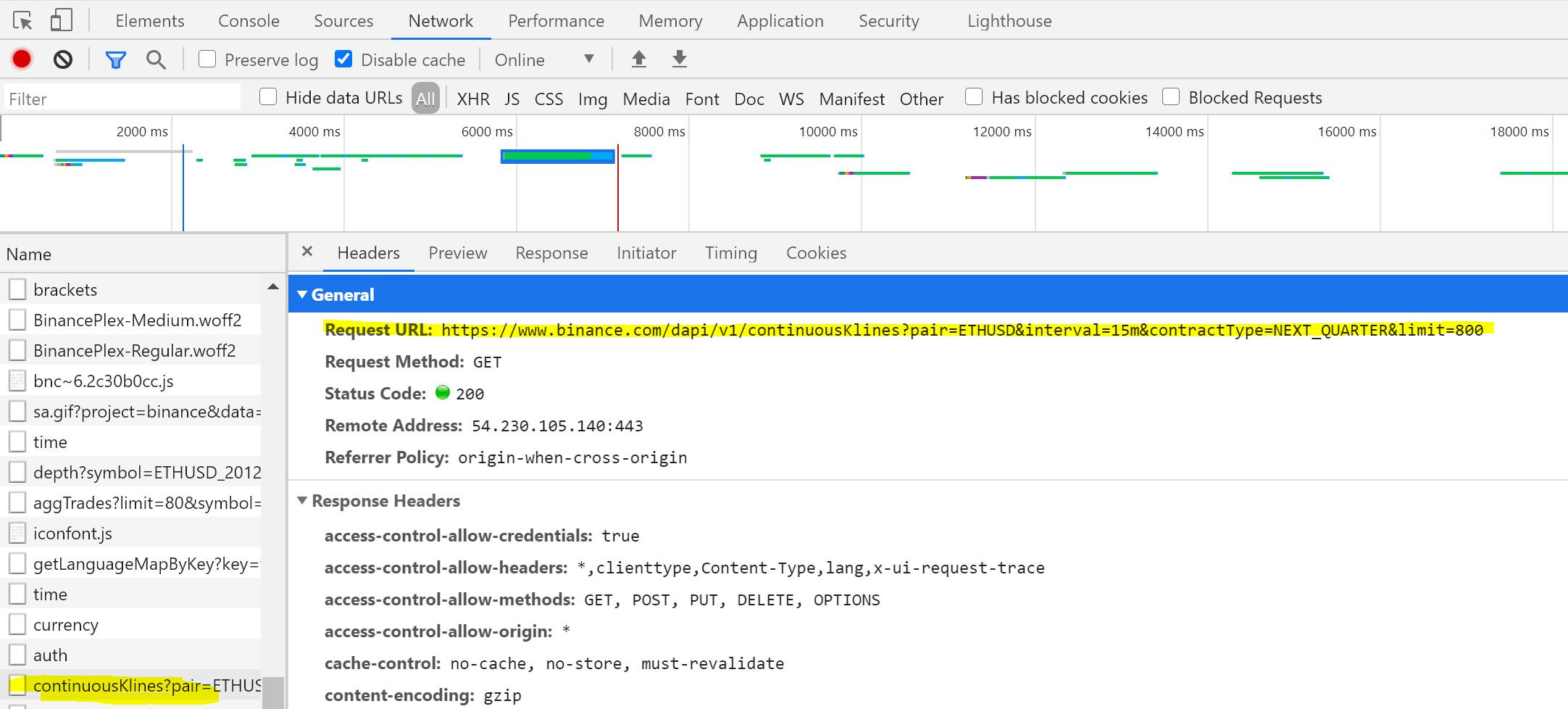
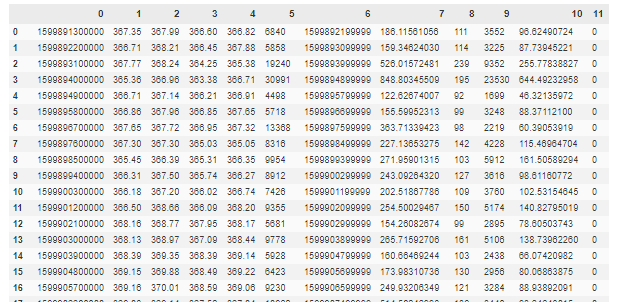
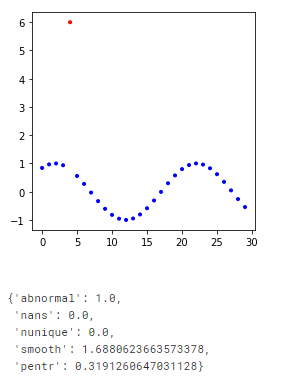
Feature selection in low signal-to-noise environments like finance.
In the following we will create a feature selection function which would work on XGBoost models as well as Tensorflow and simple sklearn models.
We will use univariate as well as other state of the art selection methods such as boruta,sequential feature elimination and shap values.
It’s important ot notice that in noisy environments different feature selection methods (and even same method, run twice) will not usually produce same sets of features.
Thus we will measure weighted tau rank correlation between sets of features produced by different methods and same methods , but on train and test sets.
We will use weighted and not simple tau correlation to emphasize top ranked features.
Feature selection is usually the most time-consuming step in machine learning applications, thus we will be logging the progress to file using python logging module.
Another point to mention is that it’s useful to add non-informative “noise” features into the set of actual features, and then look into rank position of these noise features to measure the performance of the the feature selection algorithm.
For univariate feature selection we would recommend just using distance correlation (to measure non-linear dependence effects) and pearson correlation (for linear dependence) , as other methods, such as Fisher F-test, Chi2 and tau and spearman correlations would give similar results.
We will use the following python packages:
pip install xgboost
pip install logging
pip install mlextend
pip install eli5
pip install pyentrp
The function signature will be the following:
def runselector(df,y,xs,model,nansy,nansx,methods=None,scoring=None,eval_metric=None,verbose=0,cv=None,eliniter=5,dftest=None):
where df is a dataframe (train set)
y is column name for y variable (we predict y ~ xs )
xs is list of feature column names.
nansy = NaN’s substitution rule for y
nansx NaN’s substitution rule for features
methods = list of feature selection methods
scoring = scoring function (i.e. f1)
cv = cross validation iterator
eliniter = number of iterations for eli method
dftest = test dataset (optional)
We will also make this function to work with sklearn’s pipelines, useful when features need scaling, and to avoid information leak from scaling whole dataset.
To run univariate feature selection inside feature selector we will use help function fs1().
def fs1(res,y,xs=None):
if xs is None:
xs=res.columns
xs=list(xs)
xs=list(set(xs)-set([y]))
df=res[xs+[y]]
dcors={}
pearsons={}
fctests={}
frtests={}
chi2abs={}
mir={}
mic={}
kendalls={}
for col in xs:
dfdropna=df[[col,y]].replace([np.inf, -np.inf], np.nan).dropna()
if dfdropna.shape==(0,2):
continue
try:
fctests[col]=f_classif(dfdropna[[col]],dfdropna[y])[0]
except:
pass
dcors[col]=dcor(dfdropna[col],dfdropna[y])
pearsons[col]=dfdropna[[col,y]].corr().iloc[1,0]
corrs=DF(pearsons,index=['pearsonabs']).abs().T.join(DF(dcors,index=['dcor']).T).join(DF(fctests,index=['fc']).T)
res=pd.concat([corrs,corrs.rank(pct=True).add_prefix('rk.')],axis=1).sort_values(by='rk.dcor',ascending=False)
logging.info(f"fs1 rk.dcor index {list(res['rk.dcor'].index)}")
return res
Example of usage on dummy classification problem with target variable y and features x1,x2,x3 and additional feaature q.x3 (quantile of x3 noise feature) :
from sklearn.ensemble import RandomForestClassifier
import xgboost as xgb
import numpy as np
from dcor import distance_correlation as dcor
from eli5.sklearn import PermutationImportance
from mlxtend.feature_selection import SequentialFeatureSelector
from pyentrp.entropy import permutation_entropy as pentropy
import shap
from scipy.stats import weightedtau as wtau
npa=np.array
DF=pd.DataFrame
import logging
modelxgb=xgb.XGBClassifier(objective ='binary:logistic', colsample_bytree = 1, learning_rate = 1,max_depth = 10, alpha = 1, n_estimators = 5)
x1=npa([-1,-2,-3,-4,-5,6,7,8,9,10,11,12,13,14,15])
np.random.shuffle(x1)
x2=x1+np.random.randn(len(x1))
x3=np.random.randn(len(x1))
y=(x1>0).astype(int)
xs=['x1','x2','x3','q.x3']
dfunittest=DF({'x1':x1,'x2':x2,'x3':x3,'q.x3':pd.qcut(x3,3,labels=False),'y':y})
display(fs1(dfunittest,'y',xs))
runselector(dfunittest.iloc[:10],y='y',xs=xs,model=modelxgb,nansy='.fillna(0)',nansx=None,verbose=10,methods=['sfsb','sfsf','eli','shap'],dftest=dfunittest.iloc[-10:],scoring='f1',eval_metric='auc',cv=2)
output:
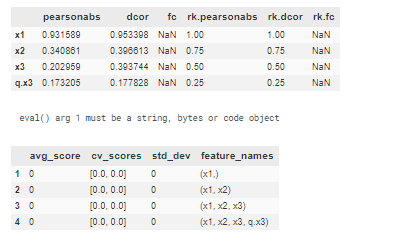
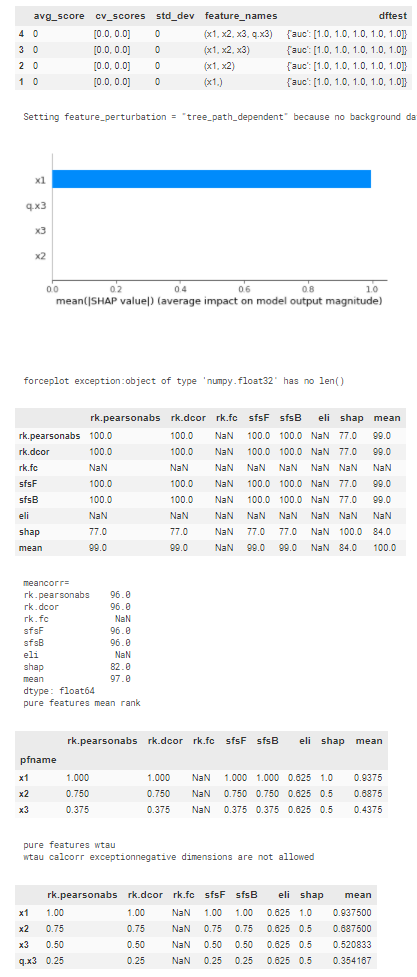
Full code of the feature selection and helper functions:
from sklearn.ensemble import RandomForestClassifier
import xgboost as xgb
import numpy as np
from dcor import distance_correlation as dcor
from eli5.sklearn import PermutationImportance
from mlxtend.feature_selection import SequentialFeatureSelector
from pyentrp.entropy import permutation_entropy as pentropy
import shap
from scipy.stats import weightedtau as wtau
npa=np.array
DF=pd.DataFrame
import logging
def calccorr(df,method='dcor',**kwargs):
#ipdb.set_trace()
if method.replace('abs','') in ['pearson','kendall','spearman']:
dfres=df.corr(method=method.replace('abs','')).rename_axis(method)
if 'abs' in method:
return dfres.abs()
else:
return dfres
cols=df.columns
resd=DF(np.zeros((len(cols),len(cols))),index=cols,columns=cols)
for icol1 in range(len(cols)):
for icol2 in range(len(cols)):
if icol1!=icol2:
dfdropna=df.iloc[:,[icol1,icol2]].dropna()
res=eval(method)(dfdropna.iloc[:,0],dfdropna.iloc[:,1],**kwargs)
if method in ['wtau']:
res=res[0]
if method in ['np.corrcoef']:
res=res[1,0]
resd.iloc[icol1,icol2]=res
else: #calc pentropy
#ipdb.set_trace()
resd.iloc[icol1,icol2]=pentropy(df.iloc[:,[icol1]].dropna().values.flatten(),order=3,delay=1,normalize=True)
return resd.rename_axis(method)
pd.core.frame.DataFrame.calccorr=calccorr
def myround2(ts):
try:
return int(np.round(float(ts),2)*100)
except: pass
try:
return (np.round(ts.astype(float),2)*100).astype(int)
except: pass
try:
return {k:(np.round(v,2)*100).astype(int) for k,v in ts.items() }
except Exception as e:
pass
return ts
pd.core.frame.DataFrame.myround2=lambda df:df.applymap(myround2)
pd.core.series.Series.myround2=lambda df:df.apply(myround2)
def fs1(res,y,xs=None):
if xs is None:
xs=res.columns
xs=list(xs)
xs=list(set(xs)-set([y]))
df=res[xs+[y]]
dcors={}
pearsons={}
fctests={}
frtests={}
chi2abs={}
mir={}
mic={}
kendalls={}
for col in xs:
dfdropna=df[[col,y]].replace([np.inf, -np.inf], np.nan).dropna()
if dfdropna.shape==(0,2):
continue
try:
fctests[col]=f_classif(dfdropna[[col]],dfdropna[y])[0]
except:
pass
dcors[col]=dcor(dfdropna[col],dfdropna[y])
pearsons[col]=dfdropna[[col,y]].corr().iloc[1,0]
corrs=DF(pearsons,index=['pearsonabs']).abs().T.join(DF(dcors,index=['dcor']).T).join(DF(fctests,index=['fc']).T)
res=pd.concat([corrs,corrs.rank(pct=True).add_prefix('rk.')],axis=1).sort_values(by='rk.dcor',ascending=False)
logging.info(f"fs1 rk.dcor index {list(res['rk.dcor'].index)}")
return res
def runselector(df,y,xs,model,nansy,nansx,methods=None,scoring=None,eval_metric=None,verbose=0,cv=None,eliniter=5,dftest=None):
try:
if 'xgb' in model.named_steps['pipe1'].__class__.__name__.lower():
if eval_metric=='f1':
eval_metric=minusf1
except:
if 'xgb' in 'xgb' in model.__class__.__name__.lower():
if eval_metric=='f1':
eval_metric=minusf1
if methods is None:
methods=['boruta','rfe','sfsb','sfsf','shap','eli']
xs=list(xs)
if scoring is None:
if df[y].nunique()<10:
scoring='balanced_accuracy'
else:
scoring='r2'
print('runselector scoring is None.using {}'.format(scoring))
ytrain=eval('df[y]'+nansy)
xtrain=eval('df[xs]'+nansx) if nansx is not None else df[xs]
try:
inferfreq=pd.infer_freq(df.index)
except:
inferfreq=None
logging.info(f"runselector START df.index.min,max={df.index.min(),df.index.max()} dftest.minmax={dftest.index.min(),dftest.index.max() if dftest is not None else 'None'} inferfreq={inferfreq} meansecsdiff= {float(np.diff(npa(df.index)).mean())/1e9}secs scoring={scoring} \n modelclass={model.__class__.__name__} modeldict={model.__dict__} xs={xs} \n {df.describe()}")
try:
model=eval(model)
except Exception as e:
print(e)
fs1df=fs1(df,y,xs)
res=fs1df[fs1df.columns[fs1df.columns.str.contains('rk\\.')]]
if 'boruta' in methods:
boruta_selector=BorutaPy(model).fit(xtrain,ytrain)#, n_estimators = 10, random_state = 0)
# boruta_selector=BorutaPy(model).fit(xtrain.values,ytrain.values)#, n_estimators = 10, random_state = 0)
boruta=DF({'boruta':boruta_selector.ranking_,'xs':xs}).set_index('xs').rank(ascending=False,pct=True).sort_values(by='boruta',ascending=False)
logging.info(f'boruta: {boruta.round(2)*100}')
res=res.join(boruta)
#boruta_selector = selectormodel
if 'abscoef' in methods:
try:
# ipdb.set_trace()
modelcoef=clone(model)
modelcoef.fit(xtrain, ytrain)
rfeselectorranking=np.abs(modelcoef.coef_[0])*xtrain.std() #multiply by feature stddev, ocnditional that feture is centered at 0
abscoef=DF({'abscoef':rfeselectorranking,'xs':xs}).set_index('xs').rank(ascending=False,pct=True)
res=res.join(abscoef)
abscoeflog=DF({'abscoefbystd':rfeselectorranking,'coef':modelcoef.coef_[0],'std':xtrain.std(),'xs':xs}).set_index('xs').sort_values(by='abscoefbystd',ascending=False)
logging.info(f'abscoef:\n {abscoeflog}')
except Exception as e:
print(f"abscoef:{e}")
if 'rfe' in methods:
try:
rfeselector = RFE(model, 1, step=1).fit(xtrain, ytrain)
rfeselectorranking=rfeselector.ranking_
rfe=DF({'rfe':rfeselectorranking,'xs':xs}).set_index('xs').rank(ascending=False,pct=True)
res=res.join(rfe)
except Exception as e:
print(f"rfe:{e}")
if 'sfsf' in methods:
sfsf = SequentialFeatureSelector(model,k_features=len(xs), forward=True, floating=False, verbose=0, scoring=scoring, cv=cv).fit(xtrain, ytrain,custom_feature_names=xs)
sfsF=DF(np.unique(DF(sfsf.get_metric_dict()).T['feature_names'].sum(), return_counts=True)).T.set_index(0).rank(pct=True).sort_values(by=1,ascending=False).rename(columns={1:'sfsF'})
if verbose>1:
display(DF(sfsf.get_metric_dict()).T[['avg_score','cv_scores','std_dev','feature_names']])
res=res.join(sfsF)
logging.info(f'sfsf:\n {sfsF.round(2)*100}')
if 'sfsb' in methods:
sfsb = SequentialFeatureSelector(model,k_features=1, forward=False, floating=False, verbose=0, scoring=scoring, cv=cv).fit(xtrain, ytrain,custom_feature_names=xs)
sfsB=DF(np.unique(DF(sfsb.get_metric_dict()).T['feature_names'].sum(), return_counts=True)).T.set_index(0).rank(pct=True).sort_values(by=1,ascending=False).rename(columns={1:'sfsB'})
if verbose>1:
sfsbd=DF(sfsb.get_metric_dict()).T[['avg_score','cv_scores','std_dev','feature_names']]
if dftest is not None:
sfsbd['dftest']=''
for i,row in sfsbd.iterrows():
if 'Pipe' in model.__class__.__name__:
model.fit(df[list(row['feature_names'])],df[y],pipe1__eval_metric=eval_metric,pipe1__eval_set=[(dftest[list(row['feature_names'])], dftest[y])],pipe1__verbose=0)
sfsbd.at[i,'dftest'] = model.named_steps['pipe1'].evals_result()['validation_0']
else:
model.fit(df[list(row['feature_names'])],df[y],eval_metric=eval_metric,eval_set=[(dftest[list(row['feature_names'])], dftest[y])],verbose=0)
sfsbd.at[i,'dftest'] = model.evals_result()['validation_0']
print(list(row['feature_names']),eval_metric,sfsbd.at[i,'dftest'])
logging.info(f"sfsbd=\n{sfsbd.myround2()}")
display(sfsbd.round(3))
logging.info(f'sfsb:\n {sfsB.round(2)*100}')
res=res.join(sfsB)
model.fit(xtrain,ytrain)
if 'eli' in methods:
if cv is None:
cv='prefit'
permuter = PermutationImportance(model, scoring=None, cv=cv, n_iter=eliniter, random_state=42)#instantiate permuter object #'balanced_accuracy' 'prefit'
elidf=DF({'eli':permuter.fit(xtrain.values,ytrain.values).feature_importances_,'xs':xs}).set_index('xs').rank(ascending=True,pct=True).sort_values(by='eli',ascending=False)
logging.info(f'eli: {elidf.round(2)*100}')
res=res.join(elidf)
if 'shap' in methods:
if 'Pipe' in model.__class__.__name__:
if 'xgb' in model.named_steps['pipe1'].__class__.__name__.lower() and model.named_steps['pipe1'].get_params()['booster'] in ('gbtree',None):
explainer=shap.TreeExplainer(model.named_steps['pipe1'],model_output='raw')
elif 'NN' in model.named_steps['pipe1'].__class__.__name__:
explainer=shap.DeepExplainer(model.named_steps['pipe1'].model.model, data=xtrain.values)#, session=None, learning_phase_flags=None)
elif 'Logistic' in model.named_steps['pipe1'].__class__.__name__:
explainer=shap.KernelExplainer(model.named_steps['pipe1'].predict_proba, data=xtrain.values, link='logit',l1_reg='aic')
else:
raise ValueError(f"shap for model {model.named_steps['pipe1'].__class__.__name__} {model.named_steps['pipe1'].get_params()} not imlemented in fs.py")
else:
if 'xgb' in model.__class__.__name__.lower() and model.get_params()['booster'] in ('gbtree',None):
explainer=shap.TreeExplainer(model,model_output='raw')
elif 'NN' in model.__class__.__name__:
explainer=shap.DeepExplainer(model.model.model, data=xtrain.values)#, session=None, learning_phase_flags=None)
elif 'Logistic' in model.__class__.__name__:
explainer=shap.KernelExplainer(model.predict_proba, data=xtrain.values, link='logit',l1_reg='aic')
else:
raise ValueError(f"shap for model {model.__class__.__name__} and params={model.get_params()} not imlemented in fs.py")
try:
shap_values = explainer.shap_values(xtrain.values)#, tree_limit=5)
concat=np.concatenate(shap_values) if type(shap_values)==type([]) else shap_values
shap_abs = np.abs(concat)
global_importances = np.nanmean(shap_abs, axis=0)
indices = np.argsort(global_importances)[::-1]
features_ranked = []
for f in range(df[xs].shape[1]):
features_ranked.append(xs[indices[f]])
shapdf=DF({'shap':global_importances},index=xs).rank(ascending=True,pct=True)
res=res.join(shapdf)
if verbose>2:
shap.summary_plot(shap_values, df[xs], plot_type="bar",class_names=model.classes_)
shap.initjs()
try:
for i in range(len(explainer.expected_value)):
display(shap.force_plot(explainer.expected_value[i], shap_values[i],df[xs]))
except Exception as e:
print(f"forceplot exception:{e}")
except Exception as e:
logging.warning(f"shaps exception = {e}")
res['mean']=res.mean(axis=1)
res=res.sort_values(by='mean',ascending=False)
if verbose>1:
logging.info(f"res.corr.mean=\n{100*res.corr().round(2)}")
display(100*res.corr().round(2))
print(f"meancorr=\n{res.corr().mean().round(2)*100}")
logging.info(f"meancorr=\n{res.corr().mean().myround2()}")
if verbose>1:
res1=res.copy()
res1['pfname']=res1.index.str.split('.').str[-1]
res1=res1.groupby('pfname').mean().sort_values(by='mean',ascending=False)#.set_index('pfname')
print("pure features mean rank")
display(res1)
logging.info(f"pure fs mean rank\n {res1.myround2()}")
print("pure features wtau")
try:
display(100*res1.calccorr(method='wtau').round(2))
logging.info(f"pure features wtau \n{res1.calccorr(method='wtau').myround2()}")
except Exception as e:
print(f"wtau calcorr exception{str(e)}")
logging.info(f"runselector complete res=\n{res.round(2)*100} {list(res.index)}")
return res
To run the feature selection on the scaled features one can use the same function and pipe as following:
model=Pipeline([("pipe0",StandardScaler()),("pipe1",xgb.XGBClassifier(objective ='binary:logistic', colsample_bytree = 1, learning_rate = 1,max_depth = 10, alpha = 1, n_estimators = 5))])
![[<<] PriceDerivatives blog](http://www.pricederivatives.com/en/wp-content/uploads/2014/03/cropped-pricederivatives-blog-logo-Copy3.png)