How to add feature interactions

Posted on by admin

Sometimes it is preferable to use simple machine learning algorithms such as logistic regression due to speed and explainability.
But usually these simple algorithms do not incorporate interactions of the features (in contrary to , say, neural networks, where sum/difference of the features is incorporated automatically, as each neuron would sum up incoming connections, and using log transform also can add product/division of the features).

Thus here we present simple way to add feature interactions into machine learning pipeline:

def addinteract(df,cols=None,inplace=False,ops=None,retfnames=False):
    df = df if inplace else df.copy()
    fnames=[]
    if cols is None:
        cols=df.columns
    if ops is None:
        ops=['sum','sub','prd']
    def sum(a,b):
        return a+b
    def sub(a,b):
        return a-b
    def prod(a,b):
        return a*b
    for i in range(len(cols)):
        for j in range(i+1,len(cols)):
            for op in ops:
                try:
                    fname=op+'('+cols[i]+','+cols[j]+')'
                    df[fname]=eval(op)(df[cols[i]],df[cols[j]])
                    fnames.append(fname)
                except Exception as e:
                    print(e)
    if retfnames:
        return df,fnames
    return df
pd.core.frame.DataFrame.addinteract=addinteract

We can use it in the following way:

xint=np.random.randint(0,10,20)
DF=pd.DataFrame
DF({'x':xint,'y':xint-1,'z':xint+2}).addinteract()

which results in:

Posted in machine learning Tagged with: ,

time series feature transformations – quantiles

Posted on by admin

For machine learning algorithms to work well, it’s usually useful to remove noise from features.For time-series this can be achieved in several ways, such as moving averages, applying sign transform, or applying low pass filter. Other, more simple way is to just apply quantilization on the features i.e. break feature values into quantiles. There are several caveats to do it in python however.When there are very few values of the feature the default behaviour of pandas’s qcut function would be to bin the values into unequal buckets. To confront this there are 2 ways:

1) rank feature values first via rank() function using ‘first’ method
2) add random noise to the feature

2nd method is more universal as it will move the features into
different quantile buckets randomly thus keeping symmetry. But in some paplication it may not matter.
To experiment with different ways to quantilize the data we can use the following function:

def addqs(df,nq=5,lags=None,cols=None,inplace=False,method='randn',retfnames=False):
    # if method=='qcut , possible that 0,5%,95%,100%  quantiles a lot of -1 , 1 instead of alot 0, randn should compensate on average
    df = df if inplace else df.copy()
    fnames=[]
    if cols is None:
        cols=df.columns
    for col in cols:
        if lags is None:
            dftemp=df[[col]]
            kwargs={}
            iloc=list(range(len(dftemp)))
        else:
            dftemp=df[col].rolling(lags)
            kwargs={'raw':False}
            iloc=-1
        if type(nq)==type([]):
            norm=(len(nq)-1)//2
        else:
            norm=(nq-1)//2
        if method=='qcut':
            res=dftemp.apply(lambda x: pd.qcut(x, nq, labels=False,duplicates='drop').iloc[iloc]-norm ,**kwargs)#pd.rank,pct=True)
        elif method=='rank':
            res=dftemp.apply(lambda x: pd.qcut(x.rank(method='first'), nq, labels=False,duplicates='drop').iloc[iloc]-norm ,**kwargs)#pd.rank,pct=True)
        elif method=='randn':
            res=dftemp.apply(lambda x: pd.qcut(x+0.0000000001*np.random.randn(len(x)), nq, labels=False,duplicates='drop').iloc[iloc]-norm,**kwargs)#pd.rank,pct=True)
        fname='q'+method+str(nq).replace("[", "").replace("]", "").replace(" ", "")+','+str(lags)+'.'+col
        df[fname]=res
        fnames.append(fname)
    if retfnames:
        return df,fnames
    return df

pd.core.frame.DataFrame.addqs=addqs
DF=pd.DataFrame

After defining this function and adding it as a DataFrame function we can use it like this:

xint=np.random.randint(0,10,20)
DF({'x':xint}).addqs(nq=3,lags=5,method='rank')

In this example we used nq (number of quantiles) = 3 and 5 lags

In the following we can compare all 3 methods of quantilization for lag=5:

We can see that randn method geenrates more equal quantiles than other methods.

and now the same 3 methods for lag=None i.e. quantilization from the start of time-series.

The code to generate previous dataframe and histograms in jupyter is the following:

lagsN=None # or 5
df=DF({'x':xint}).addqs(nq=3,lags=lagsN,method='qcut')
for lags in [lagsN]: #[None,5]
    for nq in [3]: #[0,0.05,0.95,1],
        for method in ['rank','qcut','randn']:
            df=df.join(DF({'x':xint}).addqs(nq=nq,lags=lags,method=method),rsuffix='w')#.drop(columns='x.',errors='ignore')#.set_index('x')
df=df.set_index('x')
df=df.drop(columns=df.columns[list(df.columns.str.contains('w'))])
df.hist()
Posted in machine learning Tagged with: ,

How to run sklearn’s GridSearchCV with Tensorflow keras models.

Posted on by admin

To find optimal parameters for Neural network one would usually use RandomizedSearchCV or GridSearchCV from sklearn library.

Tensorflow keras models, such as KerasClassifier, when calling fit() function does not permit to have different number of neurons.

GridSearchCV and RandomizedSearchCV call fit() function on each parameter iteration, thus we need to create new subclass of *KerasClassifier* to be able to specify different number of neurons per layer.

To create a keras model we need a function in the global scope which we will call *build_model2*.
It will build a neural network with 2 hidden layers , with dropout after each hidden layer and custom output_bias.
Output_bias is important for problems with a highly unbalanced dataset.

def build_model2(nfirst,nfeatures,nhidden1,nhidden2,dropout,output_bias,lr): 
output_bias = tf.keras.initializers.Constant(np.log([output_bias]))
model = keras.Sequential([keras.layers.Dense(nfirst, activation='relu', input_shape=(nfeatures,)),keras.layers.Dropout(dropout),
keras.layers.Dense(nhidden1, activation='relu'), keras.layers.Dropout(dropout)])
if nhidden2!=0:
model.add(keras.layers.Dense(nhidden2, activation='relu'))
model.add(keras.layers.Dropout(dropout))
model.add(keras.layers.Dense(1, activation='sigmoid',bias_initializer=output_bias))

model.compile(optimizer=keras.optimizers.Adam(lr=lr),loss=keras.losses.BinaryCrossentropy(),metrics= ['loss', 'auc', 'precision', 'recall'])
return model

Now we will create custom sklearn classifier based on keras model, which will support GridSearch with different number of neurons for hidden layers.
To avoid potential memory leaks we also create custom destructor.

from sklearn.model_selection import cross_validate
from sklearn.base import BaseEstimator,ClassifierMixin

class MyNN(BaseEstimator, ClassifierMixin):
    def __init__(self, lr=0.005,nfirst=1,nhidden1=10,nhidden2=0,dropout=0,output_bias=1,batch_size=100,epochs=10,scale_pos_weight=1):

        self.lr=lr
        self.epochs=epochs
        self.batch_size=batch_size
        self.nfirst=nfirst
        self.nhidden1=nhidden1
        self.nhidden2=nhidden2
        self.dropout=dropout
        self.output_bias=output_bias
        self.scale_pos_weight=scale_pos_weight

    def fit(self, X, y,**fit_params): ##{'nhidden': 40,'nfirst': 20,'epochs': 1,'drop2': 0.2,'drop1': 0.2,'batch_size': 100}

        try:
            if X.isnull().values.any() or y.isnull().values.any():
                print("X or y contain nans")
        except:
            pass
        self.classes_ = unique_labels(y)
        if self.scale_pos_weight is not None:
            fit_params['class_weight']={0:1,1:self.scale_pos_weight}
        self.model = KerasClassifier(build_model2,**{'nfeatures':X.shape[-1],'lr':self.lr,'nhidden1': self.nhidden1,'nhidden2': self.nhidden2,'nfirst': self.nfirst,\
                                                     'epochs': self.epochs,'dropout': self.dropout, 'batch_size': self.batch_size,'output_bias':self.output_bias},verbose=0)
        
        fit_paramsnoevalset=fit_params.copy()
        for k in ['eval_metric','eval_set']:#,entriesToRemove:
           fit_paramsnoevalset.pop(k, None)

        if fit_params.get('eval_set') is None: 
            self.history=self.model.fit(X,y,**fit_paramsnoevalset)

        else:
            self.history=self.model.fit(X,y,validation_data=(fit_params['eval_set'][0][0], fit_params['eval_set'][0][1]),**fit_paramsnoevalset) 
            if fit_params['eval_metric'] not in [m._name for m in METRICS]:
                try:
                    scorer=SCORERS[fit_params['eval_metric']]._score_func
                except:#like minusf1 
                    scorer=fit_params['eval_metric']
                self.score=scorer(fit_params['eval_set'][0][1],self.model.predict(fit_params['eval_set'][0][0]))    
            else:
                self.score=self.history.history['val_'+fit_params['eval_metric']]
        return self.model 
         
    def evals_result(self):
          return {'validation_0':self.score}
          
    def predict(self, X):
        return self.model.predict(X)
    
    def predict_proba(self, X):
        return self.model.predict_proba(X)
    
    def __del__(self):
          tf.keras.backend.clear_session()
          gc.collect()
          if hasattr(self, 'model'):
            del self.model

And now we can use MyNN model in GridSearchCV or RandomizedSearch like this (after specifying cross validation iterator via cv, and dftrain as training set, and setting scale_pos_weight for classification problem where only 10% of classes is positive):

randcv = RandomizedSearchCV(estimator=MyNN(lr=0.005,nfirst=10,nhidden1=10,nhidden2=0,dropout=0.2,output_bias=0.1,batch_size=100,epochs=1),\
                            param_distributions=dict( epochs=[ 50,100,200], batch_size=[ 10,100],nhidden1=[2,5,10],nfirst=[10,20],dropout=[0.2],output_bias=[0.1,0.9],scale_pos_weight=[1,10]),\
                            n_iter=30, scoring='f1', n_jobs=1, cv=cv, verbose=1).fit(dftrain[xs], dftrain['y'])

pd.DataFrame(randcv.cv_results_).sort_values(by='mean_test_score',ascending=False)

https://www.tensorflow.org/api_docs/python/tf/keras/wrappers/scikit_learn/KerasClassifier

Posted in machine learning Tagged with: ,

simple example simulation of delta hedging with python

Posted on by admin

Here we will present simple python code of delta hedging example of a call option .
it’s a minimal example with zero interest rates , no dividends. On day 1 we sell 10 near ATM call options and start delta hedging i.e. buying/selling stock so that change in stock price neutralizes change in options value.The portfolio is then $$\pi= delta*Stock-callOption+cashAccount$$

to simulate stock prices we will use log-normal dynamics $$ \frac{dS_t}{S_t} =\sigma_t dW_t $$

We will also simulate implied volatility as log-normal $$ \frac{d\sigma_t}{\sigma_t}=\xi dB_t $$
each day of simulation we will store in DataFrame df , so it will be easy to print and plot with pandas library.

to run the python code you will need pandas library installed in your distribution

apart from usual NPV of hedging portfolio and values of call option and greeks we will also display P&L prediction which is $$ PNL \approx \frac{\Gamma}{2} (dS)^2 + \theta dt $$

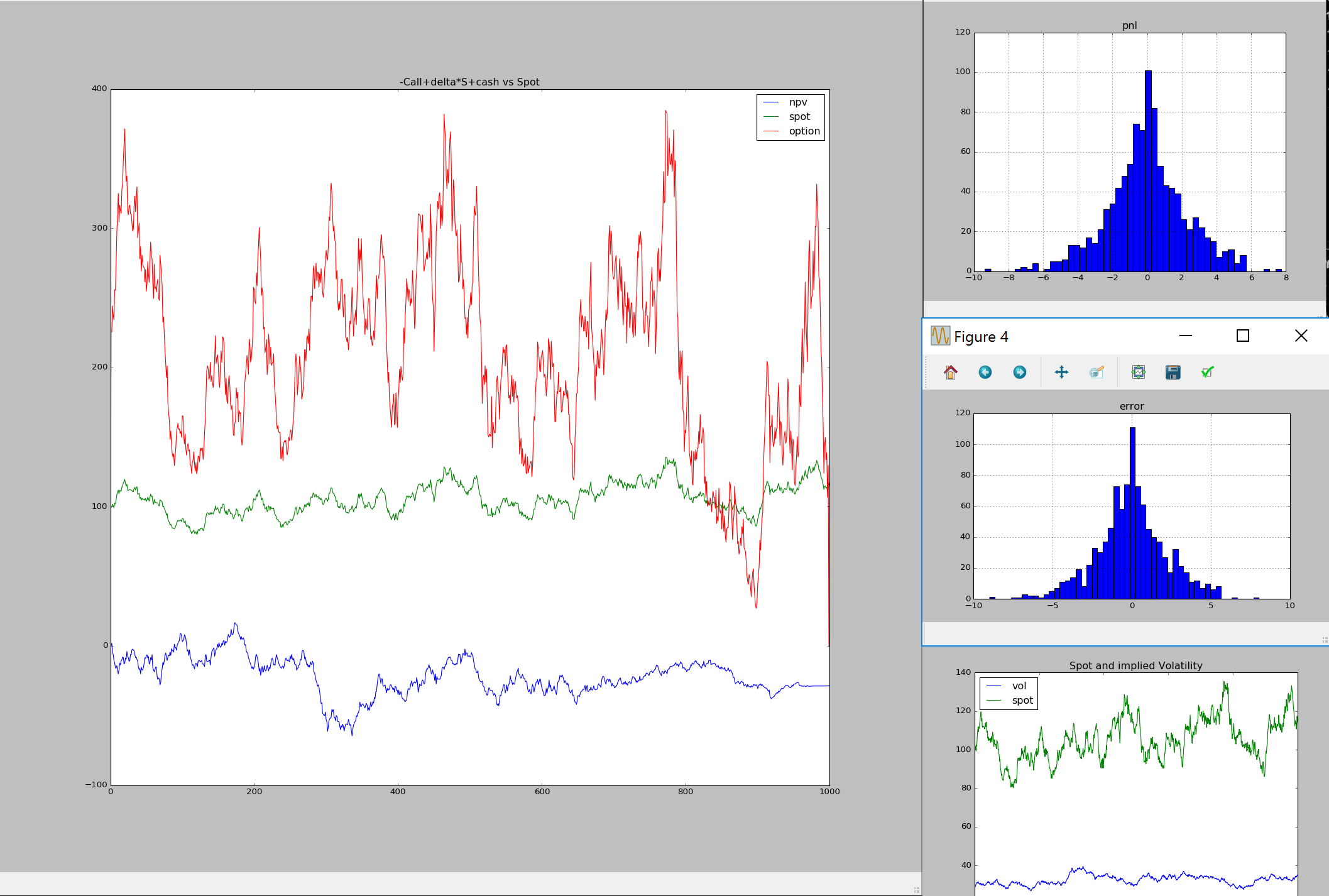
delta hedging

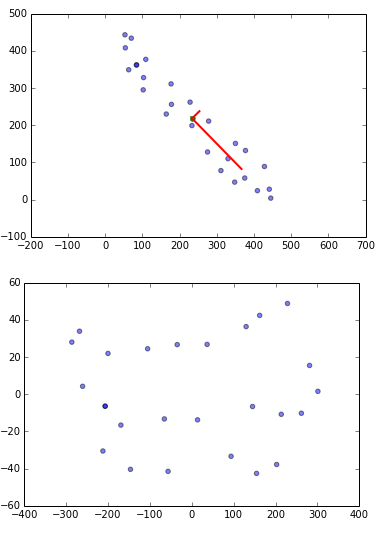
delta hedging simulation

first 10 days of delta hedging:

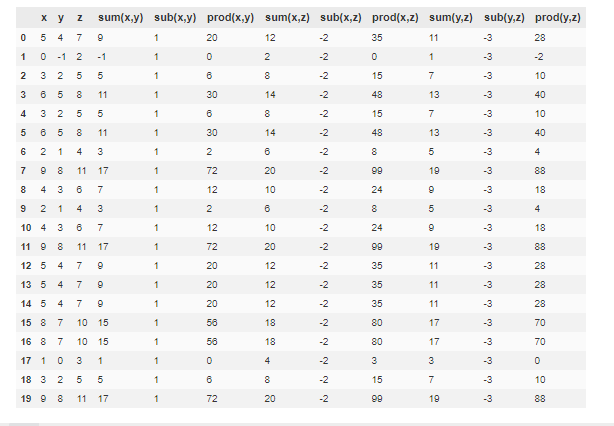
       spot   vol  shares      cash  option   npv    vega  gamma  theta  pnlPredict   pnl  error
0    100.00 30.00    0.00      0.00    0.00  0.00    0.00   0.00   0.00        0.00   nan    nan
1    102.89 29.83    6.35   -401.20  252.38  0.00 -772.52  -0.06   0.12       -0.14  0.00   0.00
2    103.65 29.89    6.40   -406.13  257.56 -0.36 -774.36  -0.06   0.12        0.10 -0.36  -0.46
3     98.00 29.34    6.02   -368.79  218.14  2.91 -754.75  -0.07   0.11       -0.96  3.27   4.23
4     96.83 29.61    5.95   -362.24  213.06  0.93 -748.61  -0.07   0.11        0.06 -1.98  -2.04
5     95.76 29.35    5.86   -353.97  204.68  2.96 -743.77  -0.07   0.11        0.07  2.03   1.96
6     95.40 28.75    5.81   -348.68  198.03  7.53 -742.86  -0.07   0.11        0.10  4.57   4.46
7     94.12 28.71    5.71   -339.71  190.26  7.85 -735.94  -0.07   0.11        0.05  0.32   0.28
8     94.28 27.96    5.69   -336.97  185.56 13.47 -737.79  -0.07   0.10        0.10  5.62   5.52
9     95.42 27.56    5.75   -343.04  189.00 16.52 -744.17  -0.07   0.10        0.05  3.05   3.00
10    96.53 28.02    5.85   -353.01  198.72 13.16 -748.41  -0.07   0.11        0.06 -3.36  -3.42

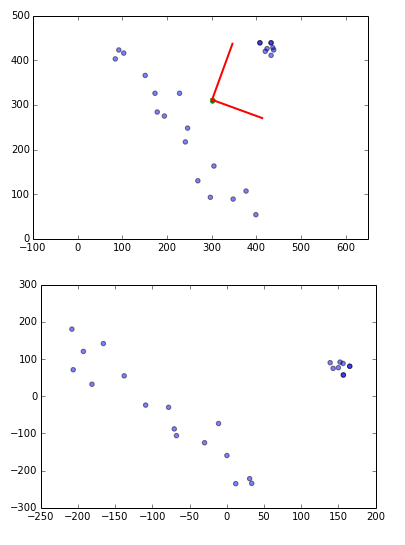
P&L profile

running this code for number of days 10,100,1000,10000 we can see P&L profile start to look narrower and more centered at 0 with number of days , in the limit of infinite days (equivalent to infinite frequency of hedging of Black Scholes assumptions) it would look like a dirac function.

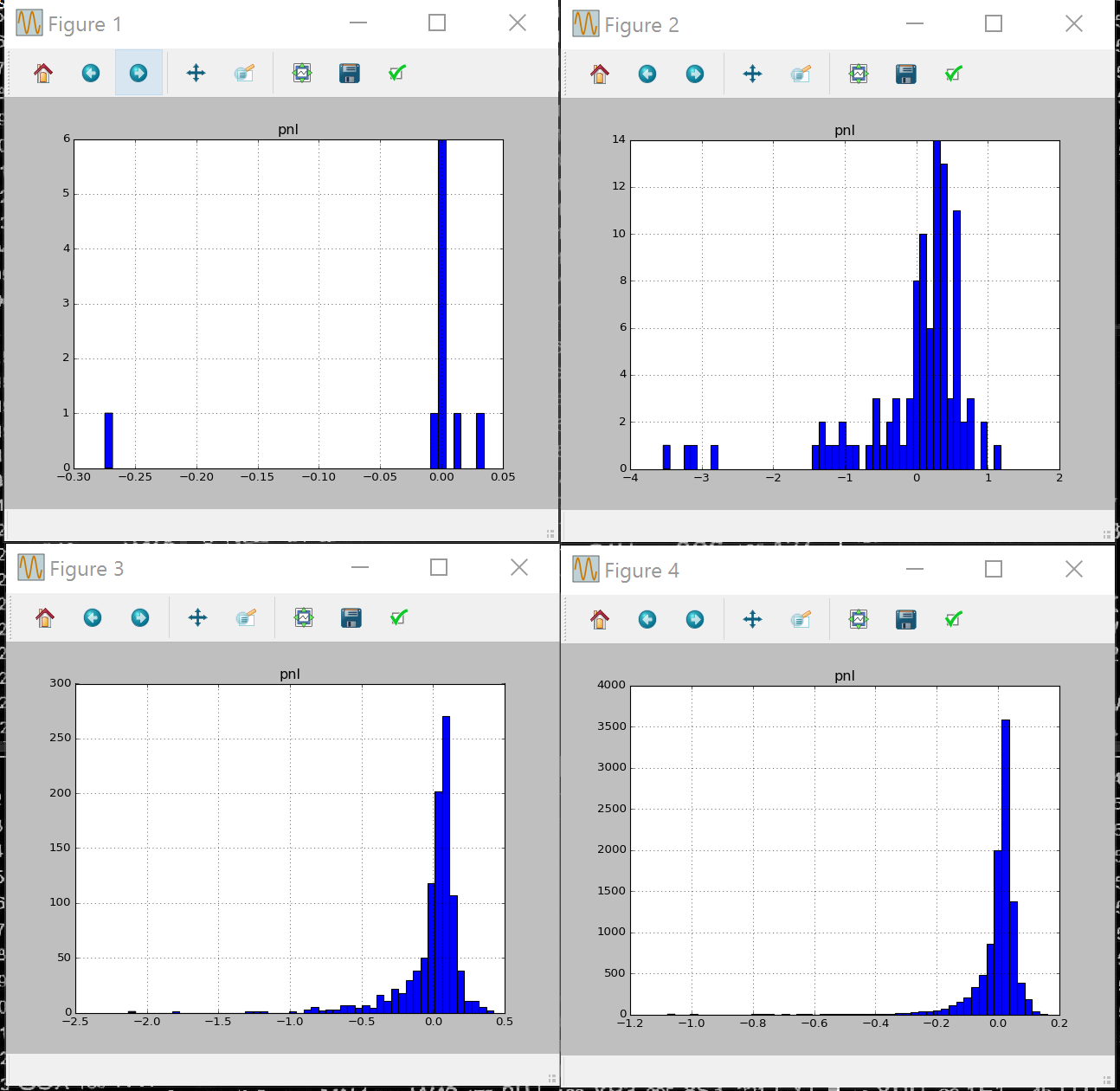
pnl profile delta hedging 10 100 1000 10000 days

pnl profile delta hedging 10 100 1000 10000 days

Why is it skewed to the left? as Gamma is always negative and high near ATM, if there’s jump down, PNL is proportional to gamma * jump size $$ PNL \approx \frac{\Gamma S^2}{2}((\frac{dS}{S})^2-\sigma^2)$$ and delta makes a high decrease, so we would need to sell many shares cheap. In case there’s a jump up, we would still need to buy more stock (as delta of call option goes up), so still would loose money in this case.That makes the daily PNL profile asymmetric.

Theta

setting Spot prices constant in the code we can see the Theta effect on the hedging strategy:
here’s the example of running the python code with constant Spot:

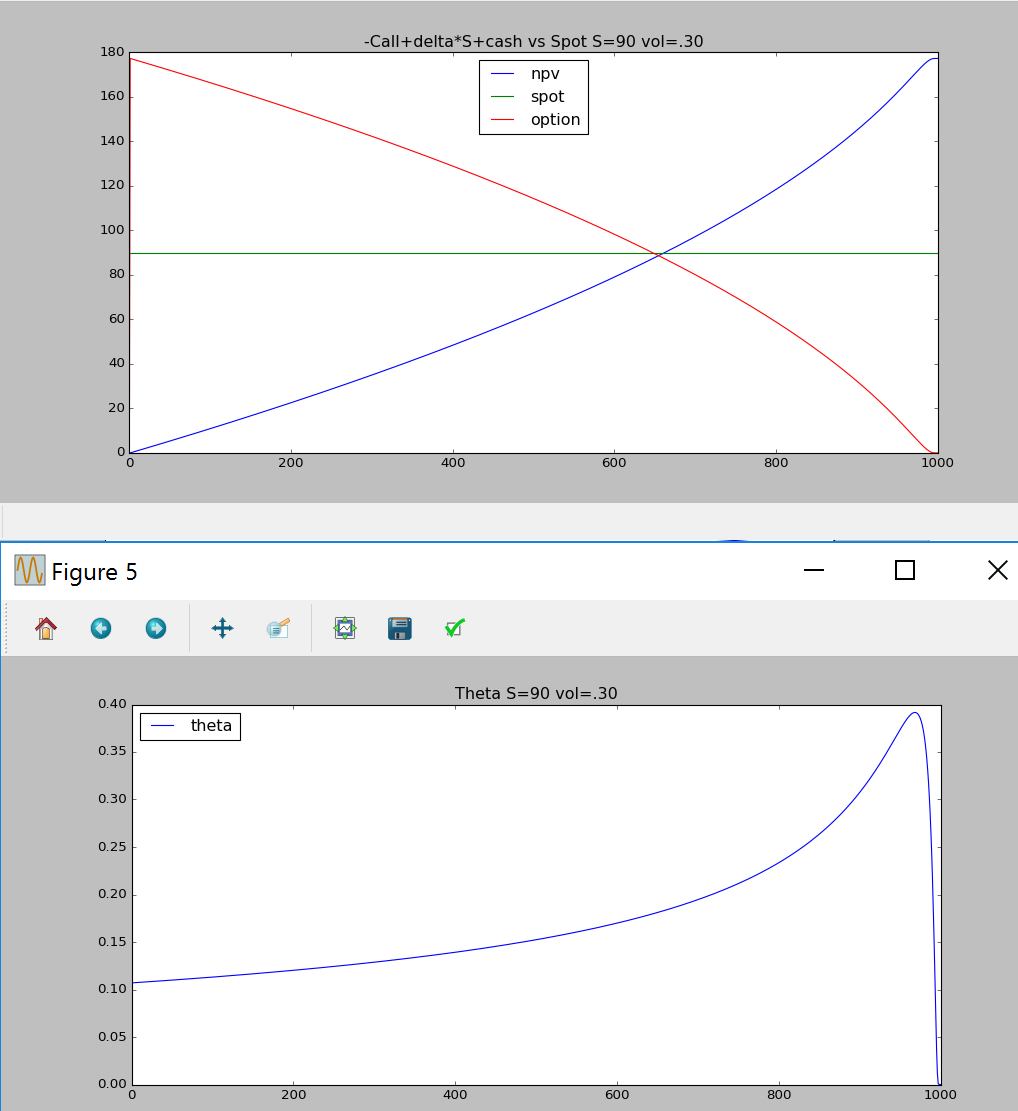
theta OTM delta hedging constant spot

theta OTM delta hedging constant spot

volaility dynamics

here we will run the code first on constant volaility , and then on stochastic implied volaility:
we can see that pnl has much wider distribution in the latter case. this is due to the fact that black sholes assumption does not hold anymore (we would need to hedge with other options to get better pnl profile)

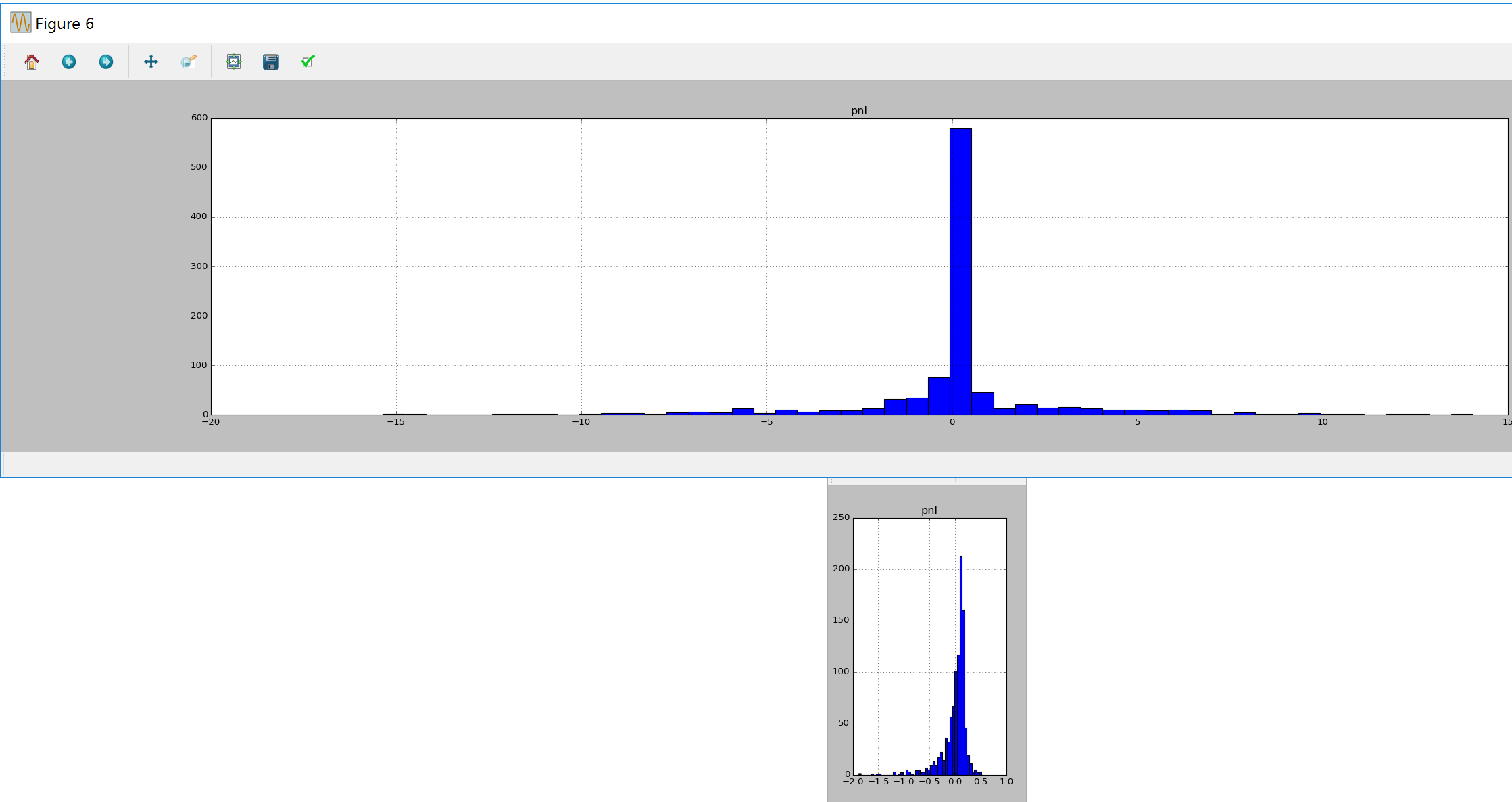
constant vs stochastic volatility

constant vs stochastic volatility pnl delta hedging

import numpy as np
import pandas as pd
pd.set_option('display.width', 320)
pd.set_option('display.max_rows', 100)
pd.options.display.float_format = '{:,.2f}'.format
from scipy.stats import norm
import matplotlib.pyplot as plt

def BlackScholes(tau, S, K, sigma):
    d1=np.log(S/K)/sigma/np.sqrt(tau)+0.5*sigma*np.sqrt(tau)
    d2=d1-sigma*np.sqrt(tau)
    npv=(S*norm.cdf(d1)-K*norm.cdf(d2))
    delta=norm.cdf(d1)
    gamma=norm.pdf(d1)/(S*sigma*np.sqrt(tau))
    vega=S*norm.pdf(d1)*np.sqrt(tau)
    theta=-.5*S*norm.pdf(d1)*sigma/np.sqrt(tau)
    return {'npv':npv,'delta':delta,'gamma':gamma,'vega':vega,'theta':theta}

class Call(object):
    def __init__(self,start,T,K,N):
        self.T=T
        self.K=K
        self.start=start  #day to sell   option
        self.N=N

    def calc(self,today,vol,S):
        if today<self.start:
            return {'delta':0,'npv':0,'vega':0,'gamma':0,'theta':0,'intrinsic':0}
        if today>self.T:
            return {'delta':0,'npv':0,'vega':0,'gamma':0,'theta':0,'intrinsic':0}
        if today==self.T:
            return {'delta':0,'npv':0,'vega':0,'gamma':0,'theta':0,'intrinsic':self.N*max(0,S-self.K)}
        tau=(self.T-today)/250.
        call=BlackScholes(tau, S, self.K, vol)
        return {'delta':self.N*call['delta'],'npv':self.N*call['npv'],'vega':self.N*call['vega'],'gamma':self.N*call['gamma'],'theta':self.N*call['theta'],'intrinsic':self.N*max(0,S-self.K)}

def deltahedge(Ndays,Sdynamics="S*=(1.0+vol*np.sqrt(dt)*np.random.randn())",volDynamics="vol=.30"):
    S=90.0
    Strike=100.0
    vol=.30
    columns=('spot','vol','shares','cash','option','npv','vega','gamma','theta','pnlPredict')
    df = pd.DataFrame([[S,vol,0,0,0,0,0,0,0,0]],columns=columns)
    dt=1/250.
    cash=0
    dayToSellCall=1
    maturityCall=Ndays-1
    call=Call(dayToSellCall,maturityCall,Strike,-10)# sell one call on dayToSellCall day
    for day in xrange(1,Ndays+1):
        exec Sdynamics
        exec volDynamics

        if day==dayToSellCall: #sell call
          callValue=call.calc(day,vol,S)
          cash-=callValue['npv']

        #delta hedge
        callValue=call.calc(day,vol,S)
        delta=callValue['delta']
        currentNumberShares=df.iloc[day-1].shares
        sharesBuy=-currentNumberShares-delta
        cash-=sharesBuy*S
        if day==maturityCall:
            cash+=call.calc(day,vol,S)['intrinsic'] #settle call

        gamma=callValue['gamma']
        theta=callValue['theta']
        dS=S-df.iloc[day-1].spot
        pnlPredict=0.5*gamma*dS*dS+theta*dt
        dfnew=pd.DataFrame([[S,vol,-delta,cash,-callValue['npv'],cash+callValue['npv']-delta*S,callValue['vega'],gamma,theta/250.,pnlPredict]],columns=columns)
        df=df.append(dfnew,ignore_index=True)

    df['pnl'] = df['npv'] - df['npv'].shift(1)
    df['vol']=100.0*df['vol']
    df['error']=df['pnl']-df['pnlPredict']
    df.set_value(dayToSellCall, "error", 0)
    #df.loc[:,['vol','spot']].plot(title='Spot and implied Volatility')
    df.loc[:,['npv','spot','option']].plot(title='-Call+delta*S+cash vs Spot {0} {1}'.format(Sdynamics,volDynamics))
    df.loc[:,['theta']].plot(title='Theta {0} {1}'.format(Sdynamics,volDynamics))
    df.loc[:,['pnl']].hist(bins=50)
    #df.loc[:,['error']].hist(bins=50)
    print df.loc[:,['pnl']].describe()
    #print df

deltahedge(1000)#constant vol
deltahedge(1000,volDynamics="vol*=(1.0+0.5*np.sqrt(dt)*np.random.randn())")#stochastic vol
deltahedge(1000,Sdynamics="S=90") #consant OTM
deltahedge(10000,Sdynamics="S=100") #consant ATM
deltahedge(10000,Sdynamics="S=110")#consant ITM
deltahedge(10000,Sdynamics="S+=S*dt") #growing stock
plt.show()
Posted in OTC derivatives valuation, quant finance coding course

python and derivatives pricing tutorial – brownian motion

Posted on by admin

In pricing models (black-scholes, local vol, libor market model) the source of uncertainty is Brownian motion. how to simulate it in python? python download

first, lets simulate dWt , we know it’s a gaussian variable with mean 0 and deviation $$ \sqrt {dt} $$
google “python gaussian” and we get to numpy gaussian
so dWt is just np.random.randn()*math.sqrt(dt)

knowing dWt how to we get to Wt at time t? $$ W_T=\int_0^T {dW_t} $$ and integral is just a sum , so $$ W_T = \sum {dW_t}$$ , so final function to calculate W_T is:

 
import numpy as np
dt=0.01
def W(T):
  sum=0
  N=T/dt
  for i in xrange(int(N)):
    sum+=np.random.randn()*np.sqrt(dt)
  return sum

now check calculate properties of brownian motion:

1) mean should be zero

 
T=1.0
nSim=10000
mean=0
for i in xrange(nSim):
  mean+=W(T)
mean/=nSim  
print mean

2) variance should be T

 
T=3.0
nSim=10000
mean=0
for i in xrange(nSim):
  wt=W(T)
  mean+=wt*wt
mean/=nSim  
print mean

now lets calculate probability $$ P( W(1)<0 and W(2) < 0) $$ 

nSim=100000
proba=0
for i in xrange(nSim):
  w1=W(1)
  w2=w1+W(1)
  if w1<0 and w2<0:
    proba+=1.
proba/=nSim  
print proba
Posted in quant finance coding course

python and derivatives pricing tutorial

Posted on by admin

Tutorial objective: write and understand simple minimal programs in python for pricing financial derivatives

topics:

Brownian motion
objective: draw and calculate properties of brownian motion using python

Black scholes pricing
objective: calculate call option price

Heston model
objective: draw forward smile as function of parameters

Libor Market model
objective: implement minimal libor market model

Markov functional model
objective: implement minimal libor markov functional model

Local Volatility model
objective: implement simplest local vol model

PDE Black Scholes
objective: implement simple PDE pricer

all topics are divided into 3 parts:
Maths,python,exercises for extension of topic

Posted in OTC derivatives valuation, quant finance coding course Tagged with: , ,

How to prepare for quantitative finance intervew

Posted on by admin

FreshPaint-0-2016.04.11-09.12.29

If you apply for quant analyst/quant developer job at investment bank/ hedge fund your quantitative finance interview will generally consist of 4 parts:

  • Programming (C++,python,data structures)
  • General probability/calculus questions
  • Stochastic calculus
  • Derivatives pricing questions for asset class (equity derivatives,interest rate derivatives,credit derivatives)

Programming

usually 2 types of questions are asked:
– data structures questions (ex. how to construct queue using only 2 stacks,how to sort array)
– specific programming questions , usually it will be C++ or Python.

best ways to prepare for programming part interview is to write small programs and debug them to see the order of execution and variable’s content. this could be very useful (copy paste programs from tutorials to your IDE and debug them)

C++ questions usually would focus on your understanding of virtual functions mechanism,shared pointers and inheritance. so the best way to prepare is to write several minimal programs using derived and base class, and then debug the code to see what constuctor, destructor or member functions get executed.
also get familiar to const , mutable , auto keywords. typical question would be to implement shared pointer from scratch – look here for interview-style implementation

Python questions would usually include pythonic ways to do simple summations on dictionaries , yield keyword and closures. again, best way to prepare is to write minimal programs of different ways to sort array, traverse tree and debug them.

data structures questions would need from you understanding of common data structures (stack, queue, tree) and basic algorithms to work with them. one of the best resourses on this topic is coursera princeton course on algorithms and data structures

questions on data structures usually would involve deriving most optimal method in terms of speed , get familiar with O(N) notation and speed of common algorithms (quicksort, bubble sort, merging of arrays)

Probability/calculus questions

get to know well Bayes theorem and solve few dozens of exercises involving it.Calculus questions usually are about calculating integrals and solving simple differential equations.
a lot of questions would involve calculating conditional expectation, so prepare by solving few dozens exercises on discrete and continuous version of conditional expectation.

Stochastic calculus

these questions would need you to demonstrate good knowledge of Ito lemma and martingale theory,remember by heart single and 2-dimensional Ito formula, and then derive differentials for common processes like W^2 , W^3 ln(S_t) exp(S_t) where S_t is black-scholes diffusion.

on questions involving same brownian motion at different times , remember that these points are jointly gaussian and use conditional expectation and variance results

Derivatives pricing questions

even if you interview for interest rate quant positions chances are you would still need to know well equity derivatives , as most questions are easier formulated using stock prices.
you would need to be confident deriving Black scholes equation using PDE and Expectation / Change of measure method. tipical questions would include calculating prices of Call,binanry options in black sholes and binomial tree model.get familiar with Local Volatility and Stochastic volatility heston model, some questions would involve qualitative price differences of , say , barrier options using both models (main thing to remember here is that in local volatility case forward skew is flatter than in stochastic volatility case), get familair with lookback option hedging argument by Gatheral (google “gatheral lookback”).

For Interest rate derivatives Girsanov theorem would invariably come in the interviews so learn how to derive Libor in arrears and CMS convexity adjustment using change of measure. Bermudan swaption pricing in one factor or libor market models can come up, so learn how to qualitativley estimate its price based on mean reversion/correlation.

for credit positions its useful to know how to derive NPV of floating and fixed leg of CDS, and poisson process characteristics.implementation of Credit Valuation Adjustment is discussed here :

Summary

Review your quant finance courses to understand basic concepts very well.debug line by line common implementations of algorithms, and practice on your phone using our app: Quant Finance Test. if you can solve all of these questions in under 5 minutes you are good to go.

Posted in OTC derivatives valuation Tagged with: , , ,

PCA simple example (principle component analisys)

Posted on by admin

simple examples of what PCA does with 2D set of points:
ellipsoid like set of points:

pca example

pca example

upper graph is original set of points
red vectors are PCA components scaled by explained variance
buttom graph is transformed set of points

so one can see that PCA will

1) move center of axis to mean of points
2) find axis with most variance.set second axis will be perpendicular to first one
3) project points to new axis

results with small outlier: (outlier make PCA less useful)

pca example outlier

pca example outlier

pca simple example python code to play with PCA:

[copy paste it to ipython enviroment with sklearn-kit installed]

press left mouse button to add points to 2D set
press right mouse button to generate PCA of points

from Tkinter import *
import numpy as np
from sklearn.decomposition import PCA

points=np.zeros((1,2))

def leftbutton(event):
    global points
    event.widget.create_oval(event.x,event.y,event.x+5 ,event.y+5,fill="red" )
    points[0][0]=event.x
    points[0][1]=event.y
    points=np.append(points,[[event.x,event.y]],axis=0)

def rightbutton(event):
    pca = PCA()
    pca.fit(points)
    traint=pca.transform(points)
    scatter(points[:,0],points[:,1],alpha=0.5)
    pmean=np.mean(points,0)
    axis('equal')
    plot([pmean[0]],[ pmean[1]], 'g.', markersize=10.0)
    S=sqrt(pca.explained_variance_)
    plot([pmean[0],pmean[0]+S[0]*pca.components_[0][0]],[pmean[1],pmean[1]+S[0]*pca.components_[0][1]],'r-',lw=2)
    plot([pmean[0],pmean[0]+S[1]*pca.components_[1][0]],[pmean[1],pmean[1]+S[1]*pca.components_[1][1]],'r-',lw=2)
    show()
    scatter(traint[:,0],traint[:,1],alpha=0.5)
    show()
    print "pca vector=",pca.components_
    print "0,0->",pca.inverse_transform([0,0])

root = Tk()
cnv = Canvas(root, bg="white", width=500, height= 500)
cnv.pack()
cnv.bind("<Button-1>", leftbutton)
cnv.bind("<Button-3>", rightbutton)
root.mainloop()
Posted in math Tagged with: ,

Libor in arrears convexity adjustment simple example

Posted on by admin
Libor in arrears

Libor in arrears

simplified Libor in arrears payoff: pay at time 1 1-year Libor reset at time 1 F(1)

$$ \frac{NPV(0)}{P_1(0)}=\mathbb{E}^1 (\frac{F(1)}{P_1(1)}) $$

where $$\mathbb{E}^1$$ is measure with numeraire $$P_1(t)$$
change measure from time 0 to time 1 (time while F(t) is changing)
with girsanov formula :

$$ \frac{P_1(0)}{P_1(1)}dP_1=\frac{P_2(0)}{P_2(1)}dP_2 $$

so we get

$$ NPV(0) = P_2(0) E^2 ( \frac{F(1)}{P_2(1)})$$

but $$ \frac{1}{P_2(1)}=1+F(1) $$

so $$ NPV(0)=P_2(0)\mathbb{E}^2(F(1))+P_2(0)\mathbb{E}^2(F^2(1)) $$

under $$\mathbb{E}^2$$ F(1) is martingale i.e. $$\mathbb{E}^2 F(1)= F(0)$$

to calculate $$\mathbb{E}^2(F^2(1)) $$ we must introduce dynamics for F(1)

for example black-scholes where under $$\mathbb{E}^2$$ : $$dF(t)=\sigma F(t) dW_t$$

so $$ F(1)=F(0) e^{\sigma W_1 – 0.5 \sigma^2 } $$ and therefore

$$ \mathbb{E}^2 F^2(1)=F^2(0) e^{-\sigma^2 } \mathbb{E}^2 e^{2 \sigma W_1 } = F^2(0) e^{\sigma^2 } $$

for CMS convexity adjustment use linear model i.e. $$ \frac{P_{->T_{mat}}}{Annuity}=A+B(T_{mat})*Swaprate $$

libor in arrears will depend on volatility as at time 1 we can reinvest this cashflow with rate F obtaining at 2 F(1+F)=F+F*F which is a nonlinear smooth function so can be decomposed into Forward plus portfolio of caplets which depends on vol

Posted in OTC derivatives valuation Tagged with:

set up global include and lib dirs in visual studio 2012

Posted on by admin

1) open any project
go to View->Property Manager

global include lib dir visual studio

global include lib dir visual studio

2) pick up any project and choose DEBUG/RELEASE wi32/win64 configuration -> Microsoft.Cpp.Win32.user file

choose VC++ directories and add desired Include and Lib dirs to appropriate section (in this case boost dirs)

property manager visual studio

property manager visual studio

Microsoft.Cpp.Win32.user configuration file is added globally to all projects

Posted in quantlib Tagged with: