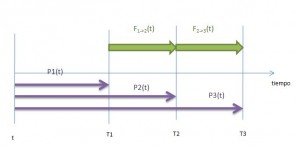
Libor Market Model is a model where Libor forwards have log-normal distribution in their’s respective probability measures (called T-measure)
example of Libor Market Model with just 2 forwards:
$$ P_3(t)$$ is a price at time t of zero-coupon bond paying at $$T_3$$
$$ F_{T_1->T_2}(t)$$ is Libor forward [fixing $$T_1$$, maturity $$T_2$$]
lets take a numeraire=bond $$P_3(t)$$
in LMM forward $$ F_{T_2->T_3}(t)$$ is martingale i.e. it has the following dynamics in the $$P_3(t)$$ measure de:
$$ dF_{2->3}(t)=F_{2->3}(t) \sigma_2 dW_2(t) $$
from this dynamics we could deduce the Black formula for caplet $$T_2->T_3$$
[this is the formula which is used by market , that why Libor market model]
forward $$F_{1->2}$$ is not a martingale anymore and will have a drift
$$ dF_{1->2}(t)=F_{1->2}(t) ( drift(t) + \sigma_1 dW_1(t) )$$
Browinan motions $$W_1(t) and W_2(t)$$ are usually correlated
$$ dW_1(t)dW_2(t)=\rho dt $$
this drift(t) can be calculated (idea : $$ (1+\delta F_{1->2} ) (1+\delta F_{1->2}) $$ must be martingale )
once we have a formula for drift we could simulate the simultanious dynamics of both forwards with monte-carlo and calculate any payoff dependend on these forwards
– long jumps
as drift depends on forwards to simulate long jumps first project forwards with F(0) values , get F(T) then use 0.5(F(0)+F(T)) as constant forwards in drift to get F(T) second time
![[<<] PriceDerivatives blog](https://www.pricederivatives.com/en/wp-content/uploads/2014/03/cropped-pricederivatives-blog-logo-Copy3.png)