Part 4

c++ finance course

Monte-Carlo c++ – Path-dependent payoffs

Objective

– price asian option with c++
– price lookback option

here we’ll show how to extend previous programs to price path dependent payoffs

Asian Option

lets start with asian option:
lets consider following asian payoff:

$$ payoff=(\frac{1}{T}\int_0^T S_t dt – K)^+ $$

1) instead of calculating the integral we’ll calculate average price of Stock S
2) to compute the average we’ll subdivide interval of time [0..T] in N parts each dt apart

0–dt–2td–3dt–…. T

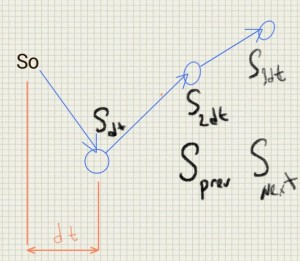
we’ll have to simulate every path time step by time step
to go from previous time step to next one by black scholes dynamics (interest rates=0 for simplicity)

$$S_0=100$$
$$S_{dt}=S_0 exp( -0.5 \sigma^2 dt + \sigma \sqrt{dt} x )$$
$$S_{next}=S_{prev} exp( -0.5 \sigma^2 dt + \sigma \sqrt{dt} x )$$

monte carlo c++

here comes the code for asian option:

#include <boost/random/variate_generator.hpp>
#include <boost/random/mersenne_twister.hpp>
#include <boost/random/normal_distribution.hpp>
#include <iostream>


double pp(double x) //positive part   x+   
{
if(x>0) return x;
return 0;
}

void main()
{

	boost::mt19937 mt; 
    boost::normal_distribution<> distribution;
    boost::variate_generator<boost::mt19937&,boost::normal_distribution<>>* normal(new boost::variate_generator<boost::mt19937&,boost::normal_distribution<>>(mt,distribution));
	
	int numberSimulations=1000;

	double S0=100.0;
	double sigma=0.2;
	double T=1.0;
	double K=100.0;
	double sum=0;
	double payoff=0;
	double NT=100;
	double dt=T/NT;
	
	for(int iSim=0;iSim<numberSimulations;iSim++) //outer loop for simulations
	{
		double Sprev=S0;
		double Snext=0;
		double averageSum=0;

		for(double t=0;t<=T;t+=dt) //inner loop for constructing one stock price path from time 0 to T
		{
			double x=(*normal)();
			Snext=Sprev*std::exp(-0.5*sigma*sigma*dt+sigma*std::sqrt(dt)*x);
			averageSum+=Snext;
			Sprev=Snext;
			//std::cout<<"\n"<<Snext; output to console of stock dynamics
		}

		payoff=pp(averageSum/NT-K);
		sum+=payoff;
	}
	
	
	std::cout<<"\nCall="<<sum/numberSimulations<<std::endl;
	
	int dummy;std::cin>>dummy;
}

in this example code we use a common construct for path-dependent payoffs :2 monte carlo loops
one for generating one path (inner loop) and another, outer loop for Monte carlo averaging of payoff

LookBack Option

in lookback option payoff strike is minimum of the stock price path over the period
so let’s change previous program to calculate lookback option

$$payoff=(S_T-\min_{0 #include <boost/random/variate_generator.hpp> #include <boost/random/mersenne_twister.hpp> #include <boost/random/normal_distribution.hpp> #include <iostream> double pp(double x) //positive part x+ { if(x>0) return x; return 0; } void main() { boost::mt19937 mt; boost::normal_distribution<> distribution; boost::variate_generator<boost::mt19937&,boost::normal_distribution<>>* normal(new boost::variate_generator<boost::mt19937&,boost::normal_distribution<>>(mt,distribution)); int numberSimulations=1000; double S0=100.0; double sigma=0.2; double T=1.0; double K=100.0; double sum=0; double payoff=0; double NT=100; double dt=T/NT; for(int iSim=0;iSim<numberSimulations;iSim++) //outer loop for simulations { double Sprev=S0; double Snext=0; double currentMin=S0; //set current minimum stock level to initial price for(double t=0;t<=T;t+=dt) //inner loop for constructing one stock price from time 0 to T { double x=(*normal)(); Snext=Sprev*std::exp(-0.5*sigma*sigma*dt+sigma*std::sqrt(dt)*x); if(Snext<currentMin) currentMin=Snext; Sprev=Snext; //std::cout<<"\n"<<Snext<<" MIN="<<currentMin;// output to console of stock dynamics } payoff=pp(Snext-currentMin); sum+=payoff; } std::cout<<"\nLookBack Call="<<sum/numberSimulations<<std::endl; int dummy;std::cin>>dummy; }

Exercises

– introduce non-zero interest rates
– calculate lookback option where strike is maximum stock price over the period