![[<<] PriceDerivatives blog](http://www.pricederivatives.com/en/wp-content/uploads/2014/03/cropped-pricederivatives-blog-logo-Copy3.png){kind=logo}
how to caclulate fair value of interest rate swap
Online Interest Rate Swap Calculator
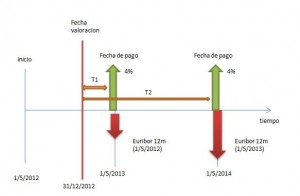
tipical example of interest rate swap contract between A and B:
example of swap
init date: 1/5/2012
maturity date: 1/5/2014
notional: 1 000 000 Eur
payments: annually
day counting convention: Actual/360
calendar: TARGET
bad day convention: Modified Following
A pays: fixed rate 4%
B pays: Euribor 12m
this contract can be represented by following cashflow diagram:
swap cashflows
Euribor rates generally are fixed at the beginning of the period (in our case one year before payment)
how to calculate fair value?
valuation algorithm
- calculate net cashflow at every paydate
- discount each cashflow to valuation date
- sum all net discounted cashflows
payment 1 (1/5/2013)
A pays 4% on 1 000 000 = 40000 eur
we must multiply this quantity by year fraction with base Act/360 = frac(1/5/2012 -> 1/5/2013) = 1.014
so finally A pays 40000*1.014=40560 eur
B pays euribor 12m fixed on 1/5/2012 [ 1.321 % ] i.e. B pays 1000000*0.01321*1.014 = 13394 eur
net pay1 = 40560 – 13394 = 27166 eur
this cashflow we must discount with EUR discount curve caclulated on 31/12/2012
suppose that discount factor for 1/5/2013 is 0.9
so discounted cashflow 1 will be 27166*0.9 = 24449 eur
payment 2 (1/5/2014)
A pays 4% on 1 000 000 = 40000 eur
multiply it by year fraction 1.014
A pays 40000*1.014=40560 eur
B pays euribor 12m fixed on 1/5/2013
this date is in the future so we must estimate it (=calculate euribor forward) with forwarding yield curve Euribor 12m on 31/12/2012
we can calculate this forward by formula:
$$ F= \frac{1}{YearFrac(1/5/2013 -> 1/5/2014)}(\frac{ DF(1/5/2013)}{DF(1/5/2014)}-1) $$
here the year fraction is calculated with the convention of the discounting curve (suppose its the same act/360 convention)
if DF(1/5/2013)=0.8
and DF(1/5/2014)=0.85
then B would pay 1000000*0.058*1.014 = 58812 eur
net pay1 = 40560 – 58812 = -18252 eur
this cashflow we must discount with the discounting yield curve with reference date 31/12/2012
suppose that discount factor( 1/5/2014)= 0.7
so discounted cashflow1 is -18252*0.7 =-12776.4 eur
So , this swap’s fair value on 31/12/2012 is -12776.4 eur
