finance c++ programming course [part 2] – numerical integration Black Scholes

part 2

black scholes via numerical integration

finance c++ course

objective

– calculate Call option in Black Scholes model using c++

C++ and QuantLib have many types of variables in quant finance most useful types are:

double – to store real number
int – to store integer number
QuantLib::Date – to store dates
QuantLib::Array – to store array of double
QuantLib::Matrix – to store 2d matrix of doubles

lets start by doing some numerical integration

delete all the contents of source.cpp file and copy paste following code

Example – numerical integration

this code will calculate integral
$$ \int_{0}^{1}e^xdx $$

#include <iostream> 
#include <cmath> //for using math functions

//everything after // is a comment

double f(double x) //declaration of function f(x)=exp(x)
{
return std::exp(x);
}

void main() 
{
	
	double dt=0.0001; //integration step
	double sum=0; //current value of integral
	for(double t=0;t<1.0;t+=dt) //for loop    t+=dt means t=t+dt
	{
	sum+=f(t)*dt; // its equivalent to write sum=sum+f(t)*dt;
	}
std::cout<<"integral "<< sum; //output

int dummy;std::cin>>dummy;//screen delay
}

read about for loop and other control structures here: http://www.cplusplus.com/doc/tutorial/control/

important notes:
use 1.0 instead of just 1
in c++ 1.0 and 1 are different numbers 1.0 is real number and 1 is integer number
it means that 1/2=0 while 1.0/2 is 0.5

when doing comparisons of doubles don’t use if(x==0)
use if( std::abs(x)for loop
see “variables scope” here http://www.cplusplus.com/doc/tutorial/variables/

here we used simplest form of numerical integration
for a faster/ more precise integratoin you can use other methods
many of them are described in free book “numerical recipes in c”
this book is for C but the code structure would be the same

example – call option in Black Scholes model using integration

now lets change previous program to calculate Call option in Black Scholes model with zero interest rates

risk-neutral dynamics:
$$ dS=S*\sigma dWt$$
so
$$ S_T=S_0 exp(-0.5 \sigma^2+\sigma \sqrt T x )$$
where x is a standard gaussian
so the call option price will be
$$ Call=\int_{-\infty}^{+\infty} (S_0 e^{-0.5 \sigma^2+\sigma \sqrt T x} – K)^+ \phi(x) dx $$
where $$\phi(x)=\frac{1}{\sqrt{2\pi}}exp(-0.5 x^2)$$ standard gaussian density
S0=100
volatility=20%
maturity=T=1 year

#include <iostream>
#include <cmath>
#include <boost/math/constants/constants.hpp>

double density(double x) //normal density 
{
	const double pi = boost::math::constants::pi<double>();
	return 1.0/sqrt(2.0*pi)*std::exp(-0.5*x*x);
}

double pp(double x) //positive part   x+   
{
if(x>0) return x;
return 0;
}

double f(double K,double S0,double T,double sigma,double x) //function to integrate  
{
return pp(S0*std::exp(-0.5*sigma*sigma*T+sigma*std::sqrt(T)*x)-K)*density(x);  
}

void main()
{
	double S0=100.0;
	double sigma=0.2;
	double T=1.0;
	double K=80.0;
	double dx=0.0001;
	double sum=0;

	for(double x=-10.0;x<10.0;x+=dx)
	{
	sum+=f(K,S0,T,sigma,x)*dx;
	}
std::cout<<"call= "<< sum;

int dummy;std::cin>>dummy;
}

Notes:

we have to pass arguments again to the integrated function because their original scope is inside main() , so variables K, S0 etc are not visible inside function f(x)
we use boost here to extract Pi constant , so it will be easier to port this program to linux for example (standard c++ has no math constants)

exercises

– debug first program by setting break points and watch variables sum and t change value
– change first program to integrate via trapezoidal rule , check the results against known answer $$ e^1-1 $$
– change second program to include non zero interest rates
– change second program to calculate put price
– verify call put parity

some tricks

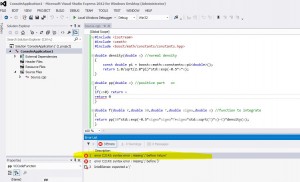
if you’ve got an error always start by correcting first compile error (double click on compile error line)
some c++ error messages are quite cryptic and are results of previous errors

for example remove “;” after return statement
press F7 to compile
now double-click on first error: